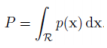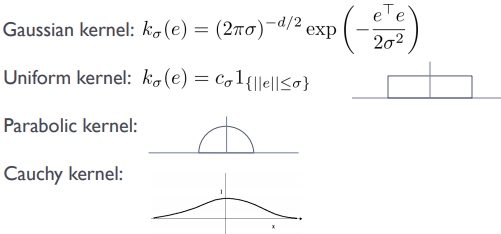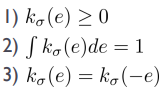Parametric distribution은 함수의 형태를 가정하고, parameter를 찾는다고 보면 된다.
Non-parametric은 분포의 형태에 대한 가정을 통해서 density estimation을 한다.
Kernel density estimation, Nearest neighbor 등의 방법이 존재한다.
Density estimation은 random variables x에 대해서 f(x)를 추정하는 방식으로 진행된다.
이 때 PDF 혹은 PMF를 이용한다.
Denstiy estimation은 regression, classification, clustering, novelty detection에 사용된다.
Non-parametric distribution은 히스토그램 기반으로 모델링을 진행한다.
이 때문에 bin width에 좌우되며, 불연속성이 존재하고, bin size가 너무 작으면 계산 비용이 크다는 문제가 있다.
또한 차원이 너무 크면 scalability issue가 발생한다.
그러나 함수 형태에 대한 가정이 필요없다는 장점이 있다.
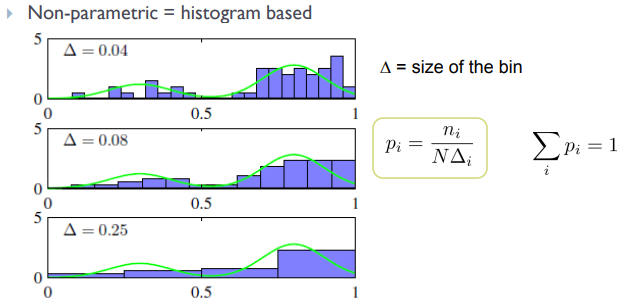
PDF에서 PMF로 변환하기 위해서는 작은 범위 R에 대해서 적분을 진행한다.
N개의 관찰이 있을 때, 범위 R 안에 K개의 포인트가 있다고 하자.
그럼 이항분포로 다음과 같이 나타낼 수 있다.
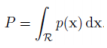


분포는 평균인 K ~ NP 근처에서 피크일 것이다.
만약 범위 R이 충분히 작다면 확률은 constant 할 것이라는 것도 알 수 있다.
따라서 확률 분포는 다음과 같이 나타낼 수 있다.


이 때 K를 고정하고 범위 V를 결정하는 것은 K-nearest neighbor 방법이라고 한다.
V를 고정하고 K를 결정하는 것은 Kernel approach라고 한다.
Kernel Density Estimation
우선 길이 h인 hypercube를 가정하고, 이에 대해 kernel function k(u)를 정의한다.
큐브 내부의 점은 1, 외부의 점은 0을 반환하는 함수인데 보통 길이는 h, 중심 위치는 x로 나타낸다.


이렇게 나타내면 가장자리에서 불연속성이 나타나는 문제가 있으므로 smoother kernel이 필요하다.
이를 위해 Gaussian을 사용하면 다음과 같이 나타낼 수 있다.


이 외에도 다른 kernel들이 존재하는데, function form에 따른 kernel function은 다음과 같다.

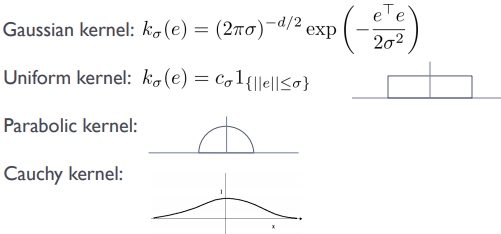
여기서 kernel function은 0보다 크거나 같아야 하고, 적분했을 때 1이며, x=0을 기준으로 대칭이어야 한다.
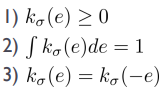
만약 kernel이 아니라 histogram으로 한다면 bin edge에서 sensitive하고, bin width에 sensitive 하다는 문제가 있다.
KDE는 training phase가 없고, training set에 대한 저장 공간만 필요하다는 장점이 있다.
그러나 다양한 단점들도 존재한다.
우선 data set size에 따라 저장 공간이 선형적으로 증가한다.
높은 차원에 대해서는 높은 계산 비용이 필요하고, 메모리 요구사항도 높다.
위에서 언급한 bandwidth 선택 문제도 존재하며, 전체 범위에서 kernel width가 고정된다는 문제도 있다.
그리고 어떤 범위에서는 높은 밀도를 보이기도 하는데, KDE는 이를 포용하지 못한다.
Nearest Neighbor Methods
위에서 언급한 것처럼 KDE는 bin width가 고정되어 특정 범위에 높은 밀도가 존재할 경우 이를 포용하지 못한다.
NN methods는 bin width를 조절하여 각 bin에 같은 수를 고정한다.
확률 분포는 위에서와 같이 p(x) = K / NV로 나타낼 수 있는데, K를 고정하고 V를 조절하는 것이다.
한 점 근처의 구 형태 내부에 몇 개의 data가 있는지를 파악하여 K개가 될 때가지 구의 영역을 넓힌다.
Density estimation, kernel smoother, regression을 통해 classification이 일어난다.
KNN은 classifier, clustering 등에 이용된다.
더보기
from elice_utils import EliceUtils
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
elice_utils = EliceUtils()
def plt_show():
plt.savefig("fig")
elice_utils.send_image("fig.png")
## Part 1: Implement Parzen Window with Gaussian Kernel
def gaussian_kernel(x, h=1.0):
# TODO: Implement the Gaussian kernel
return (1 / (h * np.sqrt(2 * np.pi))) * np.exp(-0.5 * ((x / h) ** 2))
def parzen_density_estimation(value, data, h=1.0):
# TODO: Implement the Parzen window density estimation for the given value using the provided data
density = 0
for x in data:
density += gaussian_kernel(value - x, h)
return density / (h * len(data))
# density = K/NV 이므로
## Part 2: Implement K-nearest neighhbor
def euclidean_distance(sample1, sample2):
# TODO: Compute the Euclidean distance between two samples
sample1 = np.array(sample1, dtype=float)
sample2 = np.array(sample2, dtype=float)
return np.sqrt(np.sum((sample1 - sample2) ** 2))
def knn_regression(new_sample, data, k=5):
# TODO: Predict the distance for the new grayscale value using k-NN regression
distances = [euclidean_distance(new_sample, sample) for sample in data['grayscale_value']]
sorted_indices = np.argsort(distances)
# np.argsort는 value 값에 대해서 오름차순으로, indice값을 차례로 변환
k_nearest_indices = sorted_indices[:k]
k_nearest_distances = [distances[i] for i in k_nearest_indices]
k_nearest_data = [data.iloc[i]['distance'] for i in k_nearest_indices]
prediction = np.mean(k_nearest_data)
return prediction
def main():
data = pd.read_csv("robot_vision_samples.csv")
# Visualize
values = np.linspace(min(data['distance']), max(data['distance']), 1000)
densities = [parzen_density_estimation(val, data['distance'], h=5) for val in values]
plt.plot(values, densities)
plt.title("Estimated Density of Object Distances")
plt.xlabel("Distance")
plt.ylabel("Density")
plt.show()
train, test = train_test_split(data, test_size=0.2, random_state=42)
predictions = test.apply(lambda row: knn_regression(row['grayscale_value'], train, k=5), axis=1)
mse = mean_squared_error(test['distance'], predictions)
print(f"Mean Squared Error: {mse}")
# Hyperparameter Tuning
k_values = [3, 7]
for k in k_values:
predictions = test.apply(lambda row: knn_regression(row['grayscale_value'], train, k=k), axis=1)
mse = mean_squared_error(test['distance'], predictions)
print(f"Mean Squared Error for k={k}: {mse}")
if __name__ == "__main__":
main()
더보기
import pandas as pd
from scipy.stats import norm
import numpy as np
import matplotlib.pyplot as plt
from elice_utils import EliceUtils
from scipy.stats import norm
import numpy as np
import matplotlib.pyplot as plt
elice_utils = EliceUtils()
def plt_show():
plt.savefig("fig")
elice_utils.send_image("fig.png")
# Loading data from dat.mat and p.mat
def gaussian_kernel(x, dat, h):
"""
Implement the Gaussian kernel density estimation here.
Parameters:
- x: Points where density estimation is required
- dat: Data points used for density estimation
- h: Bandwidth for the Gaussian kernel
Returns:
- p_estim: Estimated density at points x
"""
# TODO: Implement the Gaussian kernel density estimation
# Hint: Use the norm.pdf function from scipy.stats for Gaussian distribution
# Initialize the estimated density array with zeros
p_estim = np.zeros_like(x)
for i in range(len(x)):
total_kernel = 0
for j in range(len(dat)):
total_kernel += norm.pdf((x[i] - dat[j]) / h)
p_estim[i] = total_kernel / (len(x) * h)
# Loop through each data point in 'dat' and accumulate the Gaussian kernel
# Normalize the estimated density
return p_estim
def main():
# dat = loadmat("./dat.mat")["dat"].squeeze()
# p = loadmat("./p.mat")["p"]
dat = np.loadtxt("./dat.csv")
p = np.loadtxt("./p.csv", delimiter=',')
# Implementing Gaussian kernel density estimation
x = p[0, :]
p_true = p[1, :]
h = 0.5 # Gaussian kernel size h
p_estim = gaussian_kernel(x, dat, h)
# Plotting the true density and the estimated density
plt.figure(figsize=(8, 6))
plt.plot(p[0, :], p[1, :], 'g', label='True Density')
plt.plot(x, p_estim, 'b', label='Estimated Density')
plt.title(f'h={h}')
plt.legend()
plt.grid(True)
plt_show()
if __name__ == "__main__":
main()
더보기
from elice_utils import EliceUtils
from scipy.stats import norm
from scipy.io import loadmat
import numpy as np
import matplotlib.pyplot as plt
elice_utils = EliceUtils()
def plt_show():
plt.savefig("fig")
elice_utils.send_image("fig.png")
def search_vol(R, x, y, xnew):
"""
Retrieve the neighbors of xnew within a given radius R.
"""
# TODO: Implement the function to return xR and yR
# xR,yR: x_values that lie within the Radius
distances = np.linalg.norm(x - xnew, axis = 0)
indices = np.where(distances <= R)
xR = x[:, indices]
yR = y[indices]
return xR, yR
def compute_class_probablity(n, yR, V, cls_idx):
"""
Compute the probability for a given class based on the data points retrieved by the search_vol function.
n: indexes for points that belong to class 1/2/3.
yR y values that lie within the radius
V: Volume
cls_idx: Class the cluster should belong to/you want to check
"""
# TODO: Implement the function to return p for the given class
p = len(np.where(yR == cls_idx)[0] / (n * V))
return p
def main():
# Loading data from dat2d.mat
# data = loadmat("./dat2d.mat")['dat2d']
data = np.loadtxt("./dat2d.csv", delimiter=',')
x = data[0:2, :]
y = data[2, :].squeeze()
# Plotting the data
idx1 = np.where(y == 1)[0]
idx2 = np.where(y == 2)[0]
idx3 = np.where(y == 3)[0]
plt.figure(figsize=(8, 6))
plt.scatter(x[0, idx1], x[1, idx1], color='red', marker='o', label='Class 1')
plt.scatter(x[0, idx2], x[1, idx2], color='blue', marker='o', label='Class 2')
plt.scatter(x[0, idx3], x[1, idx3], color='green', marker='o', label='Class 3')
# New data point xnew
xnew = np.array([[2], [2]])
plt.scatter(xnew[0], xnew[1], color='black', marker='x', label='xnew')
# K-NN approach
R = 1
V = np.pi
xR, yR = search_vol(R, x, y, xnew)
n1 = len(idx1)
n2 = len(idx2)
n3 = len(idx3)
p1 = compute_class_probablity(n1, yR, V,1)
p2 = compute_class_probablity(n2, yR, V,2)
p3 = compute_class_probablity(n3, yR, V,3)
plt.legend()
plt.grid(True)
plt_show()
if __name__ == "__main__":
main()